1. Lý thuyết các bài toán về trung bình cộng
a. Tìm trung bình cộng của các số
Muốn tìm trung bình cộng của hai hay nhiều số, ta tính tổng của các số đó rồi lấy kết quả chia cho số các số hạng.

- Trung bình cộng = TỔNG CÁC SỐ chia SỐ CÁC SỐ HẠNG
- Nếu bài toán cho trung bình cộng và số các số hạng, thì Tổng các số = Trung bình cộng nhân Số số hạng.
- Nếu bài toán cho tổng các số hạng và trung bình cộng thì Số các số hạng = Tổng các số chia Trung bình cộng
Ví dụ 1. Tìm trung bình cộng của hai số $1$ và $17$.
Hướng dẫn.
- Ta có tổng của hai số là $1+17=18$.
- Số các số hạng là: $2$.
- Trung bình cộng của hai số đã cho là: $18:2=9$.
Ví dụ 2. Tìm trung bình cộng của các số sau: $6, 9, 13, 28$.
Hướng dẫn.
- Tổng của các số là: $6 + 9 + 13 + 28 = 56$;
- Số các số hạng là: $4$;
- Trung bình cộng của bốn số đã cho là: $56 : 4 = 14$.
Ví dụ 3. Biết trung bình cộng của ba số là $10$. Tìm tổng của ba số đó.
Hướng dẫn.
- Trung bình cộng của ba số là: $10$;
- Số các số hạng là: $3$;
- Tổng của ba số đã cho là: $10 times 3 = 30$.
Mời Quý Thầy Cô và các em học sinh xem thêm các dạng toán quan trọng và BD HSG của chương trình Toán lớp 4 và chương trình tiếng Anh lớp 4:
- Tìm hai số khi biết tổng và hiệu của hai số đó lớp 4
- BÀI TOÁN CÔNG VIỆC CHUNG LỚP 4
- Chuyên đề các dạng toán về dãy số toán lớp 4
- Toán lớp 4 – Lập số tự nhiên và quy tắc đếm
- Toán lớp 4 – Tìm số theo điều kiện cho trước
- TỔNG HỢP KIẾN THỨC VÀ BÀI TẬP TIẾNG ANH LỚP 4- 5
Ví dụ 4. Tổng các số bằng $240$ và trung bình cộng của các số là $60$. Tìm số lượng các số?
Hướng dẫn.
- Tổng của các số là: $240$;
- Trung bình cộng của các số đã cho là: $60$;
- Số các số hạng là: $240:60=4$.
b. Phương pháp giải toán trung bình cộng
- Bước 1: Xác định số lượng các số hạng có trong bài toán;
- Bước 2: Tính tổng các số hạng vừa tìm được;
- Bước 3: Trung bình cộng = “Tổng các số hạng” chia “số các số hạng có trong bài toán”;
- Bước 4: Kết luận.
Ví dụ. Trường TH Lương Thế Vinh có $3$ lớp tham gia trồng cây. Lớp 4A trồng được $17$ cây, lớp 4B trồng được $13$ cây, lớp 4C trồng được $15$ cây. Hỏi trung bình mỗi lớp trồng được bao nhiêu cây?
Hướng dẫn.
- Có lớp 4A, 4B, 4C tham gia trồng cây nên số các số hạng là $3$;
- Tổng các số hạng bằng tổng số cây mà 3 lớp đã trồng: $17 + 13 + 15 = 45$ (cây);
- Trung bình mỗi lớp trồng được số cây là: $45 : 3 = 15$ (cây).
c. Tìm trung bình cộng của các số cách đều
Để làm được các bài tập dạng này, các em học sinh cần xem thêm về dãy số cách đều trong bài Chuyên đề các dạng toán về dãy số toán lớp 4
Nếu bài viết hữu ích, bạn có thể tặng tôi 1 cốc cafe vào số tài khoản Agribank 3205215033513. Xin cảm ơn!
Ví dụ. Tính trung bình cộng của các số trong dãy số: $3,6,9,…, 105$.
Hướng dẫn. Ta đi tính tổng các số hạng dãy số trên rồi chia cho số số hạng.
- Số số hạng là: $(105 – 3) : 3 + 1 = 35$.
- Tổng các số hạng là: $( 3 +105 ) times 35 : 2 = 1890$.
- Suy ra, trung bình cộng của các số là: $$1890 : 35 = 54.$$
Đáp số: $54$.
d. Bài toán nhiều hơn trung bình cộng, ít hơn trung bình cộng
Đối với dạng toán này, chúng ta thường dùng sơ đồ đoạn thẳng để giải.
Ví dụ 1. An có $24$ cái kẹo. Bình có $28$ cái kẹo. Cường có số cái kẹo bằng trung bình cộng của ba bạn. Hỏi Cường có bao nhiêu cái kẹo?
Hướng dẫn. Theo đề bài, chúng ta có sơ đồ sau:

Nhìn vào sơ đồ ta thấy:
- Hai lần trung bình cộng số kẹo của ba bạn là: $24 + 28 = 52$ (cái)
- Trung bình cộng số kẹo ba bạn hay số kẹo của Cường là: $52 : 2 = 26$ (cái).
Đáp số: $26$ cái.
Ví dụ 2. Lan có $30$ viên kẹo, Bình có $12$ viên kẹo. Hoa có số viên kẹo lơn hơn trung bình cộng của cả ba bạn là $4$ viên. Hỏi Hoa có bao nhiêu viên kẹo.
Hướng dẫn. Ta có sơ đồ:
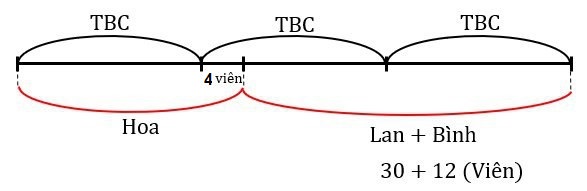
Nhìn vào sơ đồ ta thấy:
- Hai lần trung bình cộng số kẹo của ba bạn là: $30 + 12 + 4 = 46$ (cái).
- Trung bình cộng số kẹo ba bạn là: $46 : 2 = 23$ ( cái)
- Số kẹo của Hoa là: $23 + 4 = 27$ (cái).
Đáp số: $27$ cái.
Ví dụ 3. Bình có $8$ quyển vở, Nguyên có $4$ quyển vở. Mai có số vở ít hơn trung bình cộng của cả ba bạn là $2$ quyển. Hỏi số vở của Mai là bao nhiêu?
Hướng dẫn. Ta có sơ đồ:

Dựa vào sơ đồ, chúng ta có:
- Hai lần trung bình cộng số vở của ba bạn là: $8 + 4 – 2 = 10$ (quyển)
- Trung bình cộng số vở của ba bạn là: $10 : 2= 5$ (quyển)
- Số vở của Mai là: $5 – 2 = 3$ (quyển).
Đáp số: $3$ quyển.
e. Giải toán trung bình cộng bằng phương pháp “giả thiết tạm”
Phương pháp giả thiết tạm là cách thường dùng khi giải toán trung bình cộng lớp 4. Ngoài việc áp dụng các quy tắc cơ bản khi tìm số trung bình cộng ta cần đặt các giả thiết tạm thời để bài toán trở nên đơn giản hơn.
Ví dụ. Lớp 4A có 48 học sinh, lớp 4B có số học sinh nhiều hơn trung bình số học sinh của hai lớp 4A và 4B là 2 học sinh. Hỏi lớp 4B có bao nhiêu học sinh.
Hướng dẫn.
Cách 1: Phương pháp giả thiết tạm
- Nếu chuyển $2$ học sinh từ lớp 4B sang lớp 4A thì lúc này số học sinh trung bình của hai lớp vẫn không thay đổi và số học sinh mỗi lớp bằng nhau (Vì lớp 4B có số học sinh nhiều hơn trung bình số học sinh của hai lớp 4A và 4B là $2$ học sinh);
- Khi đó, số học sinh của mỗi lớp lớp là: $48 + 2 = 50$ (học sinh). Đây cũng chính là trung bình số học sinh của hai lớp.
- Suy ra, số học sinh lớp 4B là: $50 + 2 = 52$ (học sinh);
Đáp số: Lớp 4B có $52$ (học sinh).
Xem thêm Phương pháp giả thiết tạm giải toán tiểu học
Cách 2: Sử dụng sơ đồ đoạn thẳng.
Chúng ta có sơ đồ đoạn thẳng sau:

Nhìn vào sơ đồ ta thấy:
- Trung bình cộng của số học sinh hai lớp 4A và 4B là $48+2=50$ học sinh.
- Suy ra, số học sinh lớp 4B là: $50 + 2 = 52$ (học sinh);
Đáp số: Lớp 4B có $52$ (học sinh).
Quý thầy cô và các em học sinh xem thêm Phương pháp dùng sơ đồ đoạn thẳng giải toán tiểu học
2. Các ví dụ dạng toán về trung bình cộng lớp 4
Bài 1. Xe thứ nhất trở được $45$ tấn hàng, xe thứ hai trở được $53$ tấn hàng, xe thứ ba trở được số hàng nhiều hơn trung bình cộng số tấn hàng của hai xe là $5$ tấn. Hỏi xe thứ ba trở được bao nhiêu tấn hàng.
Hướng dẫn. Muốn biết xe thứ ba trở được bao nhiêu tấn hàng, ta cần tìm trung bình cộng số tấn hàng hai xe đầu trở được.
- Trung bình cộng số tấn hàng hai xe đầu trở được là: $(45 + 53) : 2 = 49$ (tấn);
- Xe thứ ba trở được số tấn hàng là: $49 + 5 = 54$ (tấn);
Đáp số: $54$ (tấn).
Bài 2. Có hai thùng dầu, trung bình mỗi thùng chứa 38 lít dầu. Thùng thứ nhất chứa 40 lít dầu. Tính số lít dầu của thùng thứ hai.
Hướng dẫn.
Bài này không yêu cầu chúng ta đi tìm trung bình cộng mà yêu cầu đi tìm số lít dầu ở thùng thứ hai. Vậy bước đầu tiên chúng ta cần tính tổng số lít dầu của cả hai thùng.
- Tổng số lít dầu ở cả hai thùng là: $38 times 2 = 76$ (lít);
- Số lít dầu của thùng thứ hai là: $76-40 = 36$ (lít).
Đáp số: $36$ (lít).
Bài 3. Tìm trung bình cộng của các số sau
a) $1, 3, 5, 7, 9$;
b) $0, 2, 4, 6, 8, 10$.
Hướng dẫn.
a) Trung bình cộng của 5 số là: $$(1 + 3 + 5 + 7 + 9) : 5 = 5.$$
b) Trung bình cộng của 6 số là: $$(0 + 2 + 4 + 6 + 8 + 10) : 6 = 5.$$
Nhận xét: Từ ví dụ trên ta thấy trung bình cộng của dãy cách đều bằng:
- Số ở chính giữa nếu dãy có số số hạng là lẻ.
- Trung bình cộng 2 số ở giữa nếu dãy có số số hạng là chẵn.
- Trung bình cộng = (số đầu + số cuối) : 2
Bài 4. Tìm 5 số lẻ liên tiếp biết trung bình cộng của chúng bằng 2011.
Hướng dẫn. Dựa vào nhận xét ở bài trước, ta dễ dàng xác định được bài toán gồm trung bình cộng của 5 số lẻ liên tiếp. Do đó trung bình cộng của 5 số này là số chính giữa.
- Số thứ 3 (số chính giữa trong 5 số) là: 2011
- Số thứ 2 là: $2011 – 2 = 2009$
- Số thứ nhất là: $2009 – 2 = 2007$
- Số thứ 4 là: $2011 + 2 = 2013$
- Số thứ 5 là: $2013 + 2 = 2015$
Bài 5. Biết tuổi trung bình của 30 học sinh trong một lớp là 9 tuổi. Nếu tính cả cô giáo chủ nhiệm thì tuổi trung bình của cô và 30 học sinh sẽ là 10 tuổi. Hỏi cô giáo chủ nhiệm bao nhiêu tuổi?
Hướng dẫn.
- Tổng số tuổi của 30 học sinh là: $9 times 30 = 270$ (tuổi).
- Số người có trong lớp kể cả cô giáo chủ nhiệm: $30 + 1 = 31$ (người)
- Tổng số tuổi của 31 người (kể cả cô giáo) là: $10 times 31 = 310$ (tuổi)
- Số tuổi của cô giáo chủ nhiệm là: $310 – 270 = 40$ (tuổi)
Đáp số: $40$ (tuổi)
3. Bài tập về trung bình cộng lớp 4
Bài 1. Tìm trung bình cộng của các số sau:
a) 10; 17 ; 24; 37 b) 1; 4; 7; 10; 13; 16; 19; 22; 25 c) 2; 6; 10; 14; 18; 22; 26; 30; 34; 38 d) 1; 2; 3; 4; 5;…; 2014; 2015 e) 5; 10; 15; 20;….; 2000; 2005
Bài 2. Trung bình cộng của 3 số bằng 25. Biết số thứ nhất là 12; số thứ hai là 40. Tìm số thứ 3.
Bài 3. Trung bình cộng của 3 số là 35. Tìm số thứ ba, biết số thứ nhất gấp đôi số thứ hai, số thứ hai gấp đôi số thứ ba.
Bài 4. Tìm 5 số chẵn liên tiếp, biết trung bình cộng của chúng bằng 126.
Bài 5. Tuổi trung bình cộng của cô giáo chủ nhiệm và 30 học sinh lớp 4A là 12 tuổi . Nếu không kể cô giáo chủ nhiệm thì tuổi trung bình cộng của 30 học sinh là 11. Hỏi cô giáo chủ nhiệm bao nhiêu tuổi?
Bài 6. An có 18 viên bi, Bình có 16 viên bi, Hùng có số viên bi bằng trung bình cộng số bi của An và Bình cộng thêm 6 viên bi, Dũng có số bi bằng trung bình cộng của cả 4 bạn. Hỏi Dũng có bao nhiêu viên bi?
Bài 7. Lân có 20 viên bi. Long có số bi bằng một nửa số bi của Lân. Quý có số bi nhiều hơn trung bình cộng của 3 bạn là 6 viên bi. Hỏi Quý có bao nhiêu viên bi?
Bài 8. Trọng lượng của năm gói hàng trong một thùng hàng lần lượt là 700g, 800g, 800g, 850g và 900g. Hỏi phải bỏ thêm một gói hàng nặng bao nhiêu gam vào thùng đó để trọng lượng trung bình của cả sáu gói sẽ tăng thêm 40g?
Bài 9. Lớp 5A và 5B trồng được một số cây. Biết trung bình cộng số cây 2 lớp đã trồng được là 235. Nếu lớp 5A trồng thêm 80 cây và lớp 5B trồng thêm 40 cây thì số cây 2 lớp bằng nhau. Tính số cây mỗi lớp đã trồng.
Bài 10. Trung bình cộng của 3 số bằng 24. Trung bình cộng của số thứ nhất và số thứ hai bằng 21, của số thứ hai và số thứ ba bằng 26. Tìm 3 số đó.
Bài 11. Trung bình cộng của 4 số bằng 25. TBC của 3 số đầu bằng 22, TBC của 3 số cuối bằng 20. Tìm TBC của số thứ hai và số thứ ba?
Bài 12. Tìm 3 số tự nhiên A, B, C biết trung bình cộng của A và B là 20, trung bình cộng của B và C là 25 và trung bình cộng của A và C là 15.
Bài 13. Trung bình cộng của 2 số bằng 57. Nếu gấp số thứ hai lên 3 lần thì trung bình cộng của chúng bằng 105. Tìm 2 số đó.
Bài 14. Khối lớp 4 của một trường Tiểu học có ba lớp. Biết rằng lớp 4A có 28 học sinh, lớp 4B có 26 học sinh. Trung bình số học sinh hai lớp 4A và 4C nhiều hơn trung bình số học sinh của ba lớp là 2 học sinh. Tính số học sinh lớp 4C?