Ở chương trình toán học lớp 6 – chương trinh toán THCS ta đã được học bài bản về số thực R. Bài viết này Bamboo sẽ giúp bạn review lại một số kiến thức và khái niệm cơ bản về số thực là gì? Các tính chất của số thực và các thuộc tính của số thực. Hãy cùng Bamboo tìm hiểu nhé!
Số thực R là gì? Định nghĩa của R trong toán học
Số hữu tỉ và số vô tỉ được gọi chung là số thực và được kí hiệu là R. Tập hợp số tự nhiên N = {0, 1, 2,…}, tập số nguyên Z = {…-3, -2, -1, 0, 1, 2,…}…tất cả các tập số này đều là tập con của R và cả các số vô tỉ như: II = 3,144592 hay = 2, 2376…Tất cả các số mà ta đã biết đều thuộc R.
Ta có: Tập hợp số thực kí hiệu là R (R=Q U I)
Tập hợp của các số thực được biểu diễn qua hình vẽ sau đây:
Trong đó:
- N: Tập hợp số tự nhiên
- Z: Tập hợp số nguyên
- Q: Tập hợp số hữu tỉ
- I = RQ: Tập hợp số vô tỉ
Vậy R là tập hợp số thực

Tính chất của R và trục số thực R
- Bất kỳ số thực khác không là số âm hoặc số dương.
- Tổng hay tích của hai số thực không âm là một số thực không âm.
- Số thực là tập hợp vô hạn các số vô cùng nhiều không đếm được các số thực.
- Có hệ thống các tập hợp con vô hạn có thể đếm được của các số thực.
- Số thực có thể được sử dụng để thể hiện các phép đo đại lượng liên tục
- Số thực có thể biểu thị bằng biểu diễn thập phân.
Các thuộc tính của tập số thực R
- Các số thực bao gồm cả các trường hợp các phép cộng và phép nhân cùng phép chia cho các số khác 0. Chúng cũng có thể được sắp xếp trên một trục hoành theo cách thương tích với phép cộng và phép nhân.
- Chúng cho biết nếu tập hợp một số thực không trống có giới hạn trên thì trên thì nó có cận trên chính là những số thực nhỏ nhất.

Ví dụ bài tập minh họa về trục số thực R
Ví dụ 1: Điền vào dấu (∈, ∉, ⊂) thích hợp vào chỗ chấm
Đáp án:
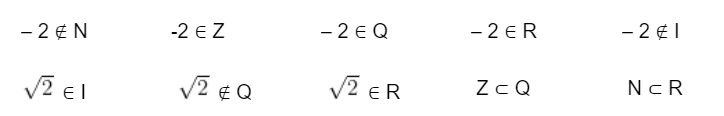
Ví dụ 2: Sắp xếp các số thực sau theo thứ tự tăng dần:
0,466 ; 7/15 ; 0,4636363…; 0,463736 ; 0,4656365…
Đáp án: 0,463763…< 0,463736 < 0,4656365…< 0,466 < 7/15
Ví dụ 3: Hãy tìm các tập hợp:
a) Q ∩ I ;
b) R ∩ I.
Đáp án:
a) Q ∩ I = Ø ;
b) R ∩ I = I
Ví dụ 4: Tìm x, biết: 3,2.x + (-1,2).x +2,7 = -4,9 ;
Giải:
3,2. x + (-1,2).x + 2,7 = -4,9
[3,2 + (-1,2)].x + 2,7 = -4,9.
2.x + 2,7 = – 4,9.
2.x = – 4,9 – 2,7
2.x = – 7,6
x = -7,6 : 2
x = -3,8
Một số tập số cần ghi nhớ
Tập hợp của các số tự nhiên được quy ước kí hiệu là N
N={0, 1, 2, 3, 4, 5, ..}.
Tập hợp của các số nguyên được quy ước kí hiệu là Z
Z={…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …}.
Tập hợp của các số hữu tỉ, được quy ước kí hiệu là Q
Q={ a/b; a, b∈Z, b≠0}
Một số hữu tỉ có thể được biểu diễn bằng một số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn.
Tập hợp của các số thực được kí hiệu là R
Mỗi số được biểu diễn bằng một số thập phân vô hạn không tuần hoàn được ta gọi là một số vô tỉ. Tập hợp các số vô tỉ được quy ước kí hiệu là I. Tập hợp của các số thực bao gồm các số hữu tỉ và các số vô tỉ.
Xem thêm:
- Cách tính trung bình cộng và các bài toán trung bình cộng cơ bản và nâng cao
- Các tính tỉ số phần trăm và các dạng toán về tỉ số phần trăm cơ bản có đáp án
- Dãy bit là gì? Dãy bit bao gồm những kí tự nào và sử dụng dãy bit để làm gì?
Với bài viết khái niệm về số thực-R trên đây, hy vọng sẽ giúp bạn nắm bắt kiến thức nhanh hơn về R trong toán học là gì? Khi ai đó hỏi bạn số thực là gì thì với những kiến thức của Bamboo đã chia sẻ trên đây sẽ giúp bạn trả lời chính xác. Chúc các bạn có một buổi học thật chất lượng nhé!!