Chúng ta đã được học về hai góc kề nhau, hai góc bù nhau, hai góc phụ nhau,… Và lên lớp 7 chúng ta sẽ được học về các góc tạo bởi một đường thẳng cắt hai đường thẳng và trong đó có góc so le trong. Vậy thế nào là góc so le trong? Làm thế nào để chúng ta có thể nhận biết được đó là góc so le trong? Các bài tập về góc so le trong có dễ làm không?… Để giải đáp thắc này thì chúng ta sẽ cùng nhau tìm hiểu bài viết dưới đây nhé.
1. Góc so le trong là gì?
– Giả sử có một đường thẳng t cắt đường thẳng q tạo thành bốn góc và cắt đường thẳng r tạo thành bốn góc. Khi đó hai góc so le trong là hai góc không chung đỉnh, nằm ở bên trong hai đường thẳng q và r và nằm ở khác phía so với đường thẳng t.
– Ví dụ minh họa:
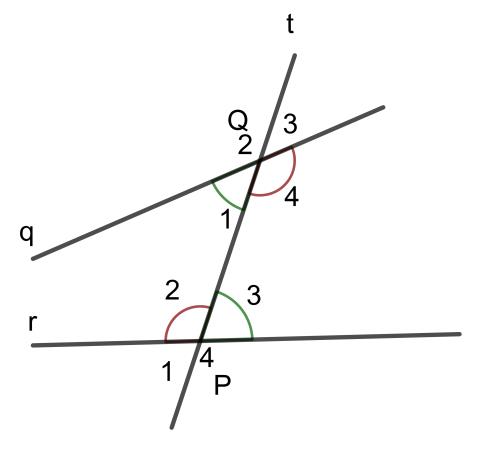
Góc Q1 và góc P3 là hai góc so le trong
Tương tự, góc Q4 và góc P2 là hai góc so le trong
2. Dấu hiệu nhận biết hai góc so le trong
Cho đường thẳng t cắt hai đường thẳng q và r tạo thành các góc. Khi đó để nhận biết được hai góc so le trong, ta dựa vào các dấu hiệu sau:
– Hai góc không được chung gốc
– Hai góc đó phải nằm ở phía trong hai đường thẳng q và r.
– Hai góc đó phải nằm ở vị trí so le nhau, hay nói cách khác, hai góc đó phải nằm ở khác phía so với đường thẳng t.
Cụ thể như sau:
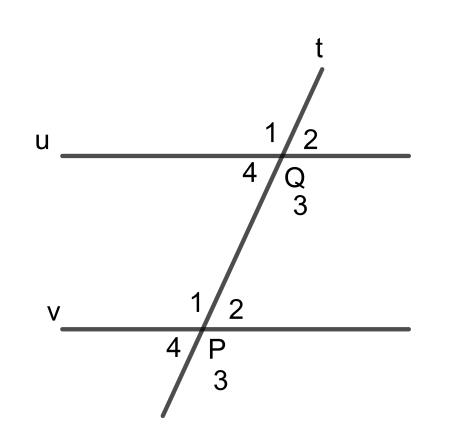
Từ hình vẽ trên, ta thấy các góc Q3, Q4, P1, P2 là các góc nằm ở phía trong hai đường thẳng u và v.
Góc Q1 và P3 là hai góc không chung gốc, nằm ở khác phía so với đường thẳng t nên góc P1 và T3 là hai góc so le trong.
Tương tự, ta có góc Q4 và P2 là hai góc không chung gốc, nằm ở khác phía so với đường thẳng t nên góc Q4 và P2 là hai góc so le trong.
Còn góc Q1 và P2, Q4 và P3 cũng là các cặp góc không chung gốc nhưng nằm cùng một phía với đường thẳng q nên các cặp góc đó không phải là góc so le trong.
3. Các dạng bài tập cơ bản về góc so le trong
3.1. Nhận biết hai góc so le trong
*Phương pháp giải: Dựa vào phương pháp nhận biết hai góc so le trong
*Ví dụ: Hãy chỉ ra các góc so le trong trong hình dưới đây trong các trường hợp sau:
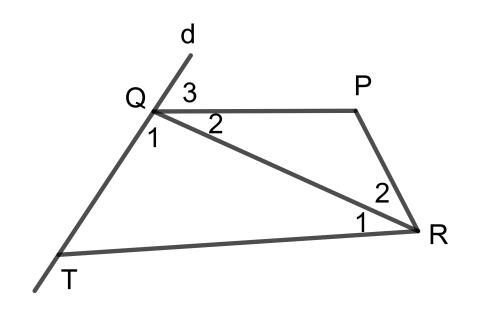
a. Đường thẳng d cắt hai đường thẳng QP và TR
b. Đường thẳng QR cắt hai đường thẳng QP và TR
c. Đường thẳng QP cắt hai đường thẳng PR và d
Giải:
a. Đường thẳng d cắt hai đường thẳng QP và TR không tạo ra cặp góc so le trong.
b. Đường thẳng QR cắt hai đường thẳng QP và TR tạo ra các cặp góc so le trong là: và , và .
c. Đường thẳng QP cắt hai đường thẳng PR và d tạo ra các cặp góc so le trong là: và
3.2. Bài tập tính số đo góc liên quan đến góc so le trong
*Phương pháp giải: Áp dụng các tính chất về hai góc so le trong, hai góc kề bù, hai góc đối đỉnh để tính số đo góc
*Ví dụ: Cho hính vẽ sau:
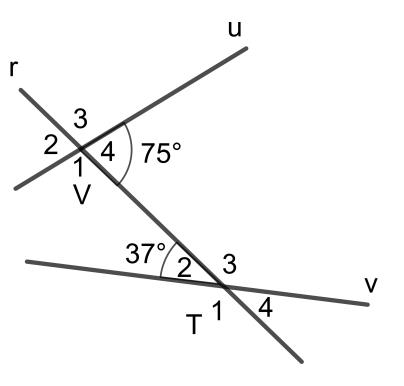
Hãy tính số đo của các góc còn lại trong hình trên
Giải:
Ta có: + = 180o (hai góc kề bù)
Mà = 75o nên:
= 180o – = 180o – 75o = 105o
Mặt khác, ta có: = = 105o (hai góc đối đỉnh)
= = 75o (hai góc đối đỉnh)
Tương tự, ta có: + = 180o ( hai góc kề bù)
Mà = 37o nên:
= 180 – = 180o – 37o = 143o
Mặt khác, ta có: = = 37o (hai góc đối đỉnh)
= = 143o (hai góc đối đỉnh)
4. Một số bài tập vận dụng về góc so le trong
Bài 1:
a. Vẽ hình theo mô tả sau:
Cho hai đường thẳng qt và zn cắt nhau tại P. Kẻ đường thẳng uv cắt hai đường thẳng qt và zn lần lượt tại N và V. Kí hiệu các góc trong hình vừa vẽ.
b. Hãy chỉ ra các cặp góc so le trong trong hình vừa vẽ trong các trường hợp sau:
Trường hợp 1: Chọn qt làm cát tuyến
Trường hợp 2: Chọn zn làm cát tuyến
Trường hợp 3: Chọn uv làm cát tuyến
ĐÁP ÁN
a. Ta có hình vẽ sau:
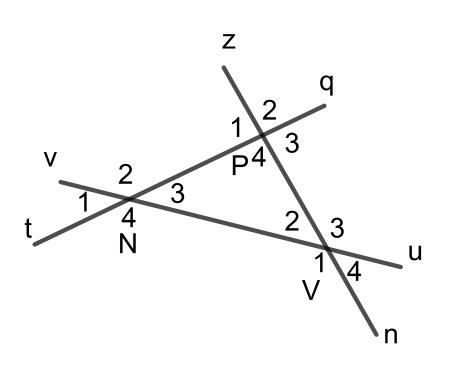
b.
Trường hợp 1: Chọn qt làm cát tuyến thì các cặp góc so le trong trong hình vừa vẽ là: và , và .
Trường hợp 2: Chọn zn làm cát tuyến thì các cặp góc so le trong trong hình vừa vẽ là: và , và .
Trường hợp 3: Chọn uv làm cát tuyến thì các cặp góc so le trong trong hình vừa vẽ là: và , và .
Bài 2:
a. Vẽ hình theo mô tả sau:
Vẽ một đường thẳng t cắt 2 đường thẳng u và v sao cho trong các góc tạo thành có một cặp góc so le trong bằng nhau và bằng 60o. Đặt tên cho các góc trong hình vừa vẽ.
b. Có tất cả bao nhiêu cặp góc so le trong? Viết tên các cặp góc so le trong đó và cho biết số đo của các góc đó.
ĐÁP ÁN
a. Vì đường thẳng t cắt 2 đường thẳng u và v và trong các góc tạo thành có một cặp góc so le trong bằng nhau nên theo tính chất của hai đường thẳng song song thì u và v song song với nhau.
Từ đó ta có hình sau:
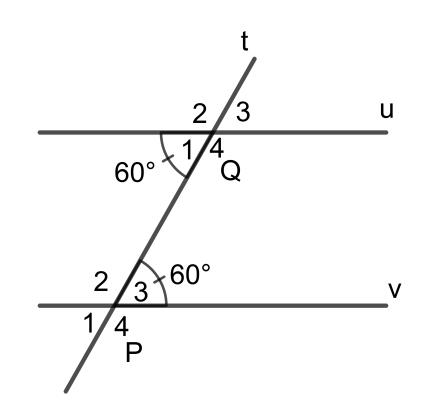
b. Có tất cả 2 cặp góc so le trong.
Tên của các cặp góc so le trong đó là: và , và .
Theo bài ra, ta có: = 60o.
Áp dụng tính chất hai đường thẳng song song, ta có: = (2 góc so le trong)
Mà = 60o nên = 60o
Ta có: + = 180o (hai góc kề bù)
Mà = 60o nên = 180o – = 180o – 60o = 120o
Tương tự, ta có: + = 180o (hai góc kề bù)
Mà = 60o nên = 180o – = 180o – 60o = 120o
Vậy số đo của các góc , , , là:
= 120o ; = 120o , = 60o và = 60o .
Trên đây là toàn bộ kiến thức về định nghĩa góc so le trong, các dạng bài tập thường gặp có phương pháp giải và ví dụ cụ thể. Bên cạnh đó, bài viết cũng đưa ra một số bài tập vận dụng kèm lời giải chi tiết và dễ hiểu. Hy vọng những kiến thức trong bài viết trên sẽ giúp các bạn học sinh hiểu rõ hơn về góc so le trong cũng như giúp các bạn trau dồi và nâng cao thêm vốn kiến thức của mình.
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang